M. C. Escher fue un artista holandés conocido por sus grabados xilográficos y litográficos que tratan sobre figuras imposibles, teselaciones y mundos imaginarios.
Los conocimientos geométricos y técnicos de los artistas islámicos fueron su fuente de inspiración. Esta cautivación le influyó en sus creaciones, que muestran una división regular del plano y sus famosos patrones de repetición, en una visión única del espacio y las matemáticas.
 |
| (Fuente: Manuel Sada Allo et al.) |
El objetivo del estudio de las teselaciones de Escher es
encontrar la estructura de una pieza que tras una sucesión de
movimientos geométricos rellene por completo el plano.
Con estas teselaciones, el alumnado puede desarrollar su abstracción y visión espacial, además de su creatividad, tomando algunas de las técnicas de Escher basadas en polígonos regulares consistentes en "deformar" algunos lados de los polígonos y llevar los cambios a los otros lados mediante traslaciones, rotaciones o reflexiones.
Además, combinando el estudio de las mismas con programas matemáticos de dibujo como Geogebra o Cabri, se contribuye a desarrollar su competencia matemática y digital, permitiendo visualizar,
experimentar y simular diferentes figuras geométricas y sus transformaciones en el plano.
En la web encontramos un sinfín de páginas didácticas dedicadas al estudio de los movimientos en el plano a través de Escher, además de al aprendizaje de la construcción de sus mosaicos y otros nuevos. Estos son algunos ejemplos:
1. Unidad didáctica de los movimientos en el plano con las teselaciones de Escher, desarrollada por Mª José Sánchez Quevedo.
2. Página interactiva sobre los mosaicos de Escher, desarrollada por Jose Manuel Arranz San José.
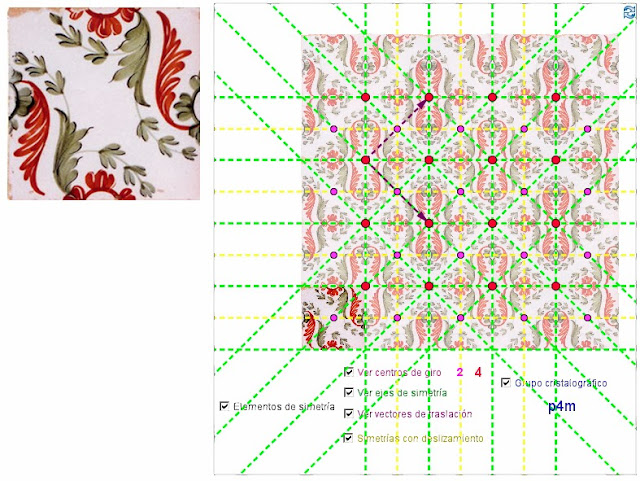
3. Colección de applets para poder encontrar los elementos de simetría de mosaicos de Escher con Geogebra, elaborados por José Antonio Mora Sánchez.
4. Página interactiva sobre los movimientos en el plano y su aplicación a los mosaicos de Escher elaborada por Ivette García Manuel.
5. Dibujo de mosaicos mediante técnicas de Escher, dentro de la página del Departamento de matemáticas del IES Arroyo.
6. Escher Picture Gallery: Archivo digital con las teselaciones de Escher.